Softmax

Introduction

Softmax is a multi-dimension version of sigmoid. Softmax is used when:

1. Used as a softer max function, as it makes the max value more pronounced in its output.

2. Approximating a probability distribution, because the output of softmax will never exceed \( 1 \) or get below \( 0 \).

Definition

softmax(\( x_i \)) = \( \frac{e^{x_i}}{\sum_j e^{x_j}} \)

With temperature

softmax(\( x_i \), \( t \)) = \( \frac{e^{\frac{x_i}{t}}}{\sum_j e^{\frac{x_j}{t}}} \)

How does softmax look, and how it works in code?

%matplotlib inline

import numpy as np
from matplotlib import pyplot as plt

def softmax(x, t = 1):
    exp = np.exp(x / t)

    # sums over the last axis
    sum_exp = exp.sum(-1, keepdims=True)
    
    return exp / sum_exp

Now let’s see how softmax approaches the max function

array = np.random.randn(5)
softer_max = softmax(array)
print(array)
print(softer_max)

[-0.75537133 -0.38787216 -0.1986      0.25125071  0.1101301 ]
[0.10750738 0.1552534  0.18760352 0.29417697 0.25545874]

See how the maximum value gets emphasized and gets a much larger share of probability. Applying weighted average would make it even clearer.

average = array.sum() / array.size
weighted = array @ softer_max
print(average)
print(weighted)
print(array.max())

-0.1960925377958444
-0.07663865446489483
0.25125071208711264

See how the weighted average gets closer to the real maximum. To make it even closer to max, reduce the temperature.

colder_max = softmax(array, 0.1)
weighted = array @ colder_max
print(average)
print(weighted)
print(array.max())

-0.1960925377958444
0.21899857608689044
0.25125071208711264

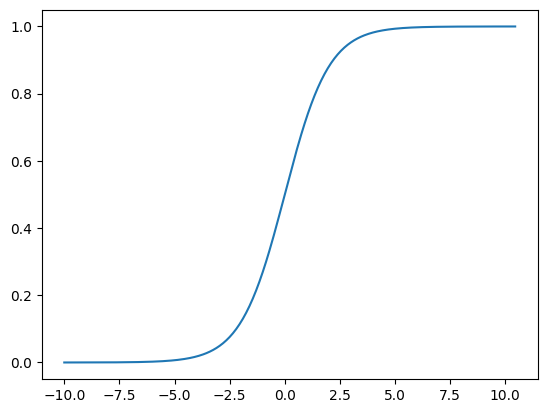
Softmax is a generalization of sigmoid. Sigmoid can be seen as softmax(\( [x, 0] \)). Plotting shows that.

x = np.zeros([410, 2])
x[:, 0] = np.arange(-200, 210) / 20
y = softmax(x)
plt.plot(x[:, 0], y[:, 0])
plt.show()